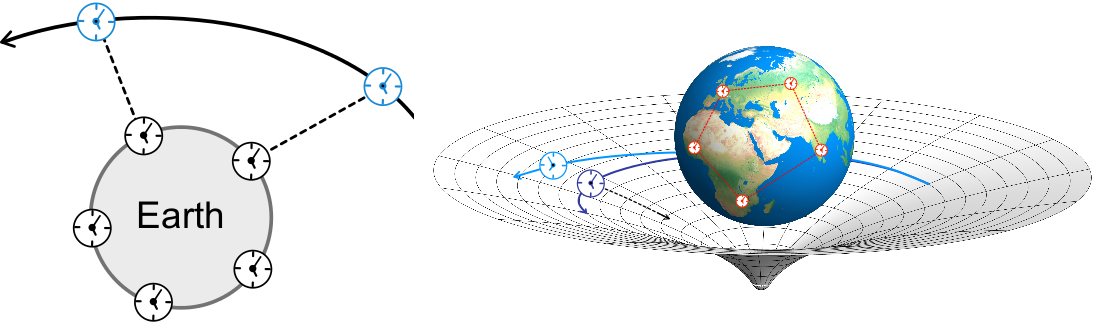
Einstein’s theory of General Relativity (GR) is presently the best available theory of gravitation. It describes the gravitational field by a curved spacetime geometry that sets the stage for all physics. So far, all conducted experiments and observations are in full agreement with the predictions of GR. The two (Newtonian) concepts of space and time now merge into a curved spacetime that differs significantly from flat Euclidean space, where gravity is described as a force in the Newtonian way.
Whereas conventional geodesy deals with Newtonian gravity, in modern relativistic geodesy General Relativity has to be considered to accurately describe clocks and their frequencies as well as satellites on their orbits. Usually, a (post-)Newtonian approximation of GR is used, which is sufficient for all applications to date. However, with the dramatic improvements in the experimental capabilities for space and ground based geodesy, it has to be critically analyzed whether the usual post-Newtonian approximations are still sufficient to fully exploit the technological level. Furthermore, deriving underlying concepts and notions within the full theory of General Relativity is more satisfactory from a methodological point of view. In this sense, we establish a top-down approach that first defines concepts, notions, relativistic effects and measurement schemes on the most general level and then employs approximation afterwards, if necessary.
The C02 project investigates this problem from two directions. First, we reconsider the definitions of fundamental geodetic quantities in the context of full General Relativity. Here, we aim at a fully relativistic definition of e.g. the Earth’s geoid that reduces to the well-known definition in the Newtonian limit. Second, we aim to improve and push forward the analytical description and calculation of relativistic effects on satellite orbits and signal propagation by using, e.g., geodesic deviation techniques, the exact timing of clocks in space, and an orbital theory based on a semianalytic Lie-series approach. Since one of the main differences between Newtonian and relativistic physics is that clocks are influenced by their state of motion and their position in curved spacetime, we also have a strong focus on the fundamental description of clocks, frequencies, clock comparison and their mutual redshifts. This includes clocks on satellites as well as clocks on the Earth’s surface and signals between them.
Results
The relativistic geoid
We found a definition of the relativistic geoid that is based on the formalism of General Relativity without approximations. For this reason, it applies not only to the Earth and other planets but also to very compact objects. This work was done in collaboration with project C03.
We define the geoid as a particular level surface of a timeindependent redshift potential. Such a potential exists in any stationary spacetime, because it is related to Killing-observers, which form an isometric congruence.
Our definition is operational because the level surfaces of a time-independent redshift potential can be realized with the help of standard clocks (clock that show proper time) and these clocks may be connected by optical fibers as well. Therefore, the equipotential surfaces are also called “isochronometric surfaces”.
We deliberately base our definition of a relativistic geoid on the use of clocks, since we believe that chronometric geodesy offers the best methods for probing gravitational fields with highest precision in the future. However, we also point out that our definition of the geoid is mathematically and operationally equivalent to a definition in terms of an acceleration potential, i.e. that our geoid may also be viewed as a level surface orthogonal to plumb lines. Thus, both independent measurements, redshifts between standard clocks and directions of plumb lines, will contribute to the determination of the relativistic geoid. Our definition reduces to the well known Newtonian and post-Newtonian notions in the appropriate limits.
Analytical description of clocks and redshifts
We analytically calculated the exact relativistic redshift between a clock on a satellite that orbits the Earth and clocks on the Earth’s surface. For now, we assumed for simplicity a radial signal transmission and describe the gravitational field of the Earth by the static Schwarzschild spacetime. With the help of our formalism, we can exactly compare the clocks on satellites with clocks on the Earth. This can also serve as a test to estimate higher order relativistic effects
We calculated the redshift between a clock on the Earth’s surface and i) radial infalling satellites ii) satellites on circular geodesic orbits and iii) satellites on arbitrary geodesic orbits. We further analyzed fully relativistic quasi-elliptic orbits in more detail and investigated the effect of the perigee precession on the redshift. The calculated redshift not only includes the gravitational redshift but also the contributions assigned to Special Relativity, that is the parallel and transverse Doppler effects; these can be seen in our results as well.
Deviation between nearby satellite orbits
Satellite missions such as GRACE and GRACE-FO are based on measuring the relative distance between two spacecraft and its temporal change along the orbit. In the context of General Relativity, in the absence of all other effects, the satellites move on timelike geodesics. The change of the (spatial) separation between two such geodesics is directly sensitive to the curvature of spacetime (the relativistic pendant to the Newtonian gravity gradient) and it is described to first order by the standard geodesic deviation equation (Jacobi equation).
The geodesic deviation equation can be used in two ways: i) to determine the curvature of spacetime by observing relative accelerations between different objects and ii) to model complex orbits as perturbations of simple reference curves. This gives a realization of the “curvature compass”.
We have investigated this equation in cooperation with project C03 for a circular reference geodesic and modeled the deviation by the solution of the Jacobi equation. Using the results, other types of orbits, such as pendulum or elliptic orbits can be constructed. We derived the connection between free parameters, that appear as integration constants, and the initial perturbation as well as the orbital elements of the perturbed orbit.
The Lie-series approach for solving EOM
In this part of the project we developed a semi-analytical Lie-series approach to calculate satellite orbits in the Schwarzschild spacetime as an initial toy model. The Lie-series approach uses the Hamiltonian that generates the equations of motion (EOM) and involves a combination of analytical and numerical techniques to solve for the orbits of satellites. Coefficients in the Lie-series are calculated by nested Poisson brackets. We compare the results with a standard Runge-Kutta integration as implemented in e.g. Mathematica, and with the exact analytical solution in terms of elliptic functions. The results show that both, the Lie-series approach and the numerical Runge-Kutta integration, differ from the exact analytical solution in the sub-nanometer regime, and even considerably less for orbits of low eccentricity. Here, we analyzed typical satellite orbit altitudes and eccentricities.
Furthermore, we plan to compare these three solution methods with the fully fledged orbit simulator XHPS, developed in project B05, which now also uses a first order post-Newtonian correction in the Newtonian equations of motion.
The semi-analytic Lie-series approach may prove very useful in relativistic spacetimes, where an analytical solution of the EOM may not exist anymore. For such situations it provides an alternative to purely numerical integration methods.
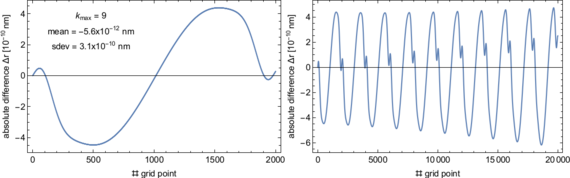
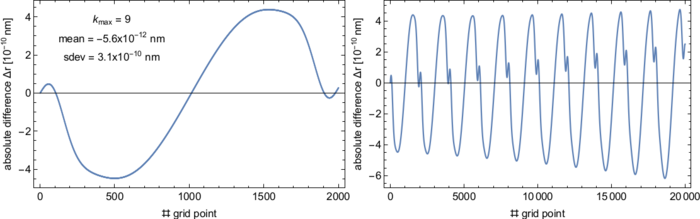
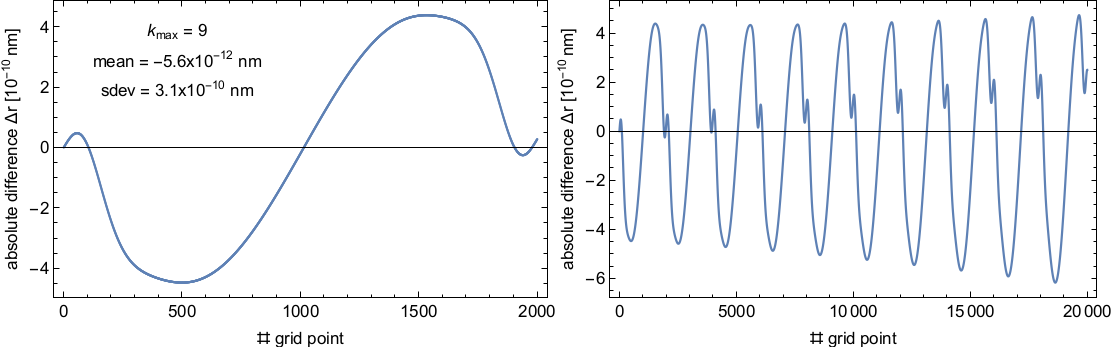
Figure 07: Radial difference between the analytical solution and the semi-analytical Lie-series approach as a function of the azimuthal angle. Here we show the result for one orbital period (left) and for the first 10 periods of an orbit similar to the one of the Galileo 5 satellite with eccentricity 0.162. We constructed over 1000 revolutions with the Lieseries approach on a grid of 2000 equally spaced points per orbit and we compared the result to the analytical solution.
Principal Investigators
Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation
Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation
Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation
Zentrum für angewandte Raumfahrttechnologie und Mikrogravitation